E5 Matlab Intro
Carr Everbach - Fall 2011
Contents
Simple math
addition
3+5
ans = 8
multiplication
3*5
ans = 15
sin() - note the argument is in radians
sin(pi/4)
ans = 0.7071
sind() - takes argument in degrees
sind(45)
ans = 0.7071
sqrt
sqrt(3)
ans = 1.7321
power
3^5
ans = 243 3^0.5
ans = 1.7321 3^1/2
ans = 1.5000
natural log (ln)
log(10)
ans = 2.3026
log base 10
log10(10)
ans = 1
pi
pi
ans = 3.1416
show more digits
format longpi
ans = 3.141592653589793
show fewer digits
format shortpi
ans = 3.1416
scientific notation
256*256*256*256
ans = 4.2950e+009
Variables - not equivalent to mathematical notation
variables go on left side. Read equals sign as "gets": x gets 3
x=3
x = 3
display value of variable
x
x = 3
note that you can't switch order.
3=x gives an error
Whatever is on left gets a new value
y=4
y = 4 x=y %This changes the value of x
%y=x would have changed value of y
x = 4
anything following a "%" sign is a comment
if you put a semicolon ";" at the end of a line, the result doesn't display.
x=5;
The above result wasn't displayed. But we can check the value of x
x
x = 5
Matrices and vectors
Row vector
a=[1 3 5 -1]
a = 1 3 5 -1
Column vector
b=[2; 4; 1; 0]
b = 2 4 1 0
Get 3rd element of each
a(3)
ans = 5 b(3)
ans = 1
Try to add
a+b
Error using ==> plus.
Matrix dimensions must agree.
define another row vector
c=[1 0 3 1]
c = 1 0 3 1
now we can add
a+c
ans = 2 3 8 0
Define a 2x2 (2 rows x 2 colums) matrix.
A=[3 5; 6 -1]
A = 3 5 6 -1
Access individual elements
A(2,1) % 2nd row, 1st column
ans = 6
Retrieve a whole column....
A(:,1) % 1st column
ans = 3 6
or a row...
A(2,:) % 2nd row
ans = 6 -1
Another matrix
B=[3 5; 5 2]
B = 3 5 5 2
Add matrices
A+B
ans = 6 10 11 1
Multiplication
A*B
ans = 34 25 13 28
Transpose (switch rows and columns)\
A
A'
A = 3 5 6 -1 ans = 3 6 5 -1
Find inverse
inv(A)
ans = 0.0303 0.1515 0.1818 -0.0909
check inverse
ans*A
ans = 1.0000 0.0000 0 1.0000
can also define identity matrix
I=eye(2)
I = 1 0 0 1
check
A*I
ans = 3 5 6 -1
Creating a range of numbers, and plotting
range of numbers
x=linspace(0,3*pi,12) %x is linearly spaced with 12 elements
x = Columns 1 through 9 0 0.8568 1.7136 2.5704 3.4272 4.2840 5.1408 5.9976 6.8544 Columns 10 through 12 7.7112 8.5680 9.4248
calculate sin()
y=sin(x)
y = Columns 1 through 9 0 0.7557 0.9898 0.5406 -0.2817 -0.9096 -0.9096 -0.2817 0.5406 Columns 10 through 12 0.9898 0.7557 0.0000
plot
plot(x,y)
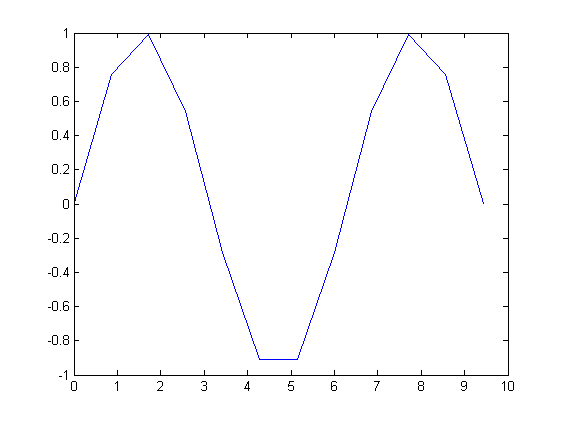
Label the plot
title('Sin(x) vs x'); xlabel('x values'); ylabel('sin(x)');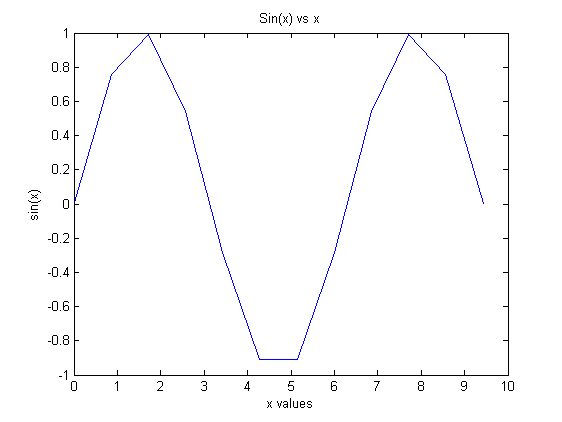
use more points
x=linspace(0,3*pi,1000);
y=sin(x);
plot(x,y,'r-.','LineWidth',2);
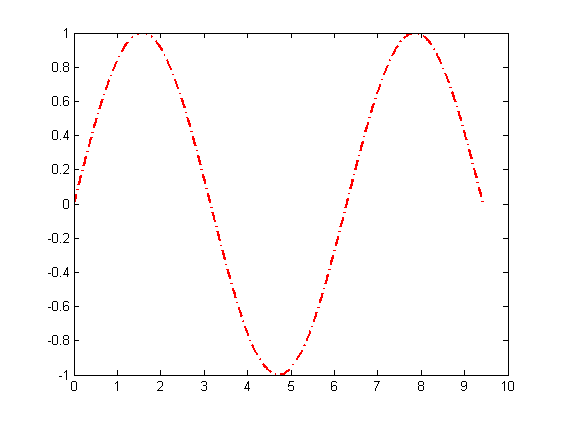
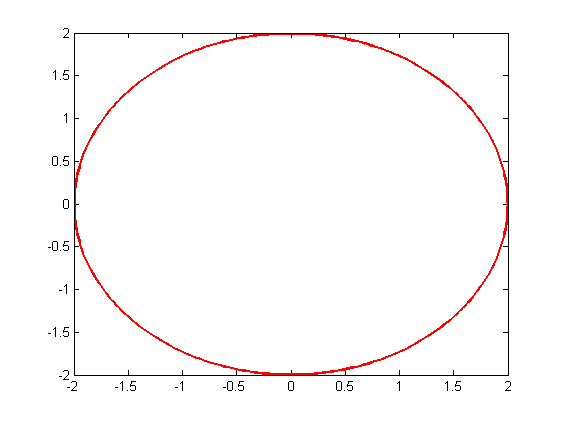
a circle (radius = 2)
theta=linspace(0,6*pi,1000);
x=2*cos(theta); y=2*sin(theta);plot(x,y,'r','LineWidth',2);
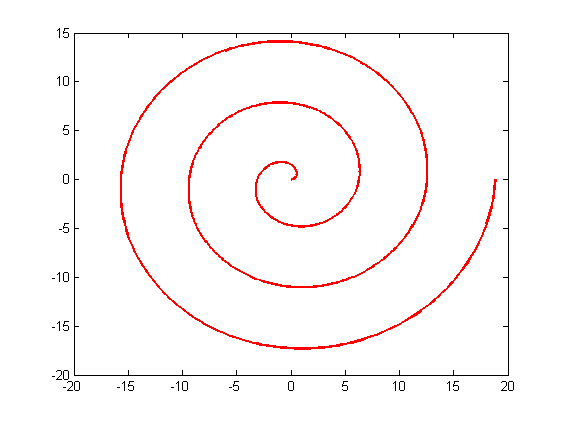
a spiral (radius=theta)
x=theta.*cos(theta); y=theta.*sin(theta);plot(x,y,'r','LineWidth',2);
a 3-D spiral with axes labeled
plot3(x,y,theta,'r','LineWidth',2);
xlabel('x'); ylabel('y'); zlabel('theta');
title('3d Spiral');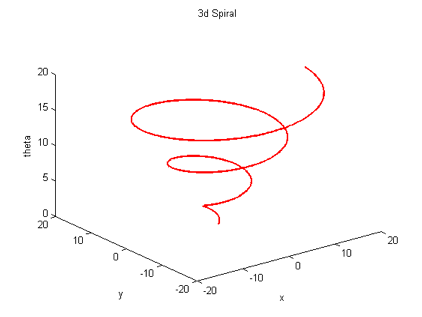
Patch graphics
Define a "patch"
clf; %clear the figure
x=[0 1 1 0];
y=[0 0 1 1];
myPatch=patch(x,y,[1 0 0]); %(x, y, color)
Set axes
axis([-5 5 -5 5]); %[xmin xmax ymin ymax]
grid
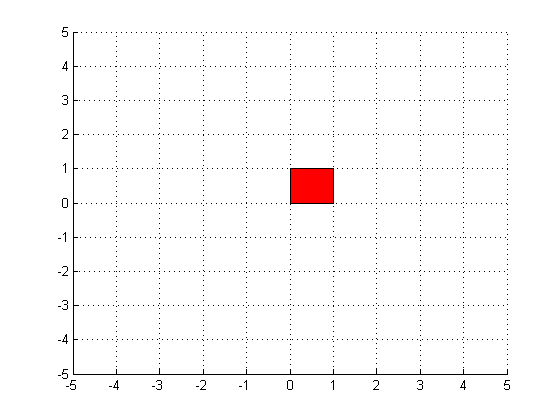
move the patch
set(myPatch,'Xdata',x+2);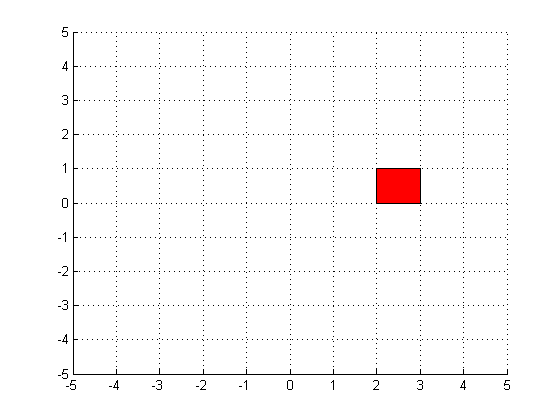
change the color
set(myPatch,'FaceColor',[0 0 1]);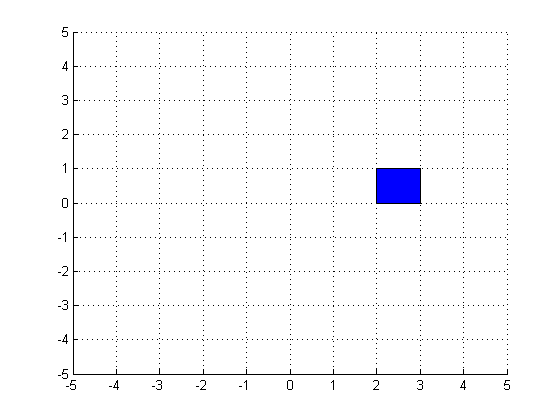
a 3d patch
x=[0 0; 1 1; 1 1];
y=[0 0; 1 -1; 0 0];
z=[0 0; 1 0.5; 0 0];
tcolor(1,1,1:3) = [1 0 0];
tcolor(1,2,1:3) = [0 1 0];
my3dPatch=patch(x,y,z,tcolor)